No time to read the whole post? I get it.

Here’s the quick and dirty resource list to get you straight to the good stuff:

image from Wale Akinfaderin, whose resources can also be found below (source: Wale Akinfaderin)

Disclaimer: These aren’t necessarily the best resources on the subject, nor have I mastered all of them. Instead, they’re the ones I’ve personally tried and liked or have been recommended by credible friends on X.

Update: about mid-way through learning Calculus 2, a friend recommended MathAcademy.com, an AI-powered platform for learning math.

I immediately fell in love due to its gamified UI, bite-sized lessons, and tremendous thought that went into picking and implementing the cutting-edge cognitive learning theory.

Frankly, I stopped consuming other math resources ever since then and just started grinding lessons on the platform.

(While I love their team, I’m not affiliated in any way.)

At the time of writing this, they’re my go-to recommendation for learning math.

That being said, they’re a paid platform (and not everyone can afford it), so I’ll do my best to present other, more standard resources below!

I highly recommend checking out this book to get an idea of everything you’ll probably need for ML: Mathematics for Machine Learning.

1. Pre-Algebra, Algebra, and Pre-Calculus: Laying the Foundation

Before you can tackle the more advanced topics, it’s crucial to get a solid grasp on the basics. This includes everything from basic arithmetic and simple equations to linear equations and logarithms. Think of this as the groundwork that will support all your future learning.

Khan Academy

The material here is easy enough, and I like the format. The only advice is to practice exercises beyond what Khan Academy provides. I’ve not read any textbooks here, so I can’t recommend more.

Pro Tip: It’s easy to overlook key areas, especially when learning on your own. Make sure to cover each topic thoroughly to avoid gaps in your knowledge later on.

2. Linear Algebra: The Backbone of Machine Learning

Mastering arithmetic is just the beginning. Now, let’s move into Linear Algebra—the backbone of almost every machine learning algorithm. This section covers vectors, matrices, determinants, eigenvalues, and linear transformations, which are all crucial for understanding how machine learning models work under the hood.

Worthy mention: I’ve seen many people recommend Prof. Gilbert Strang’s lectures, but I personally found them difficult to follow due to the low-quality video and confusing reading material.

Calculus

Next up is Calculus, where you’ll learn about limits, derivatives, integrals, and their applications. This is also where you’ll dive into functions of several variables, covering topics like partial derivatives and optimization—both critical for machine learning.

Textbooks (pick either one):

  • Calculus by Ron Larson (I used the 12th edition)
  • Calculus: Early Transcendentals by James Stewart

Courses:

Prof. Leonard’s lectures follow Ron Larson’s book, making them a perfect pair, in my opinion.

Supplemental material:

Why It Matters: It’s tempting to memorize formulas, but true understanding comes from knowing how and why these concepts work.

For example, grasping vector calculus is crucial for understanding gradient descent—a fundamental algorithm in machine learning.

Probability and Statistics

Understanding probability theory, random variables, distributions, and inferential statistics is essential for making informed decisions in machine learning. These concepts will help you understand how to handle data and make predictions.

Khan Academy: Probability and Statistics 6.041 Probabilistic Systems Analysis and Applied Probability - an amazing addition by Siddhant

Try This: Apply what you learn by analyzing a simple dataset using Python, and see how statistical methods influence machine learning outcomes.

If you have awesome resources to recommend here, let me know!

Good Channels When Stuck

Some of My Favorite Posts/Videos on Math & ML

My Math Journey So Far

In March this year, I switched from marketing to code—specifically, Machine Learning and AI.

I picked up a book called Machine Learning with PyTorch and Scikit-Learn by Sebastian Raschka and his colleagues.

The book starts with building a perceptron model, a fundamental neural network concept.

Perceptron Model: The perceptron is the simplest type of artificial neural network, with a single layer of weights connected to input features. It makes decisions by calculating a weighted sum of the inputs and passing it through a step function. If the sum is above a certain threshold, it classifies the input as one class; otherwise, it classifies it as another. It’s the basis for understanding more complex models.

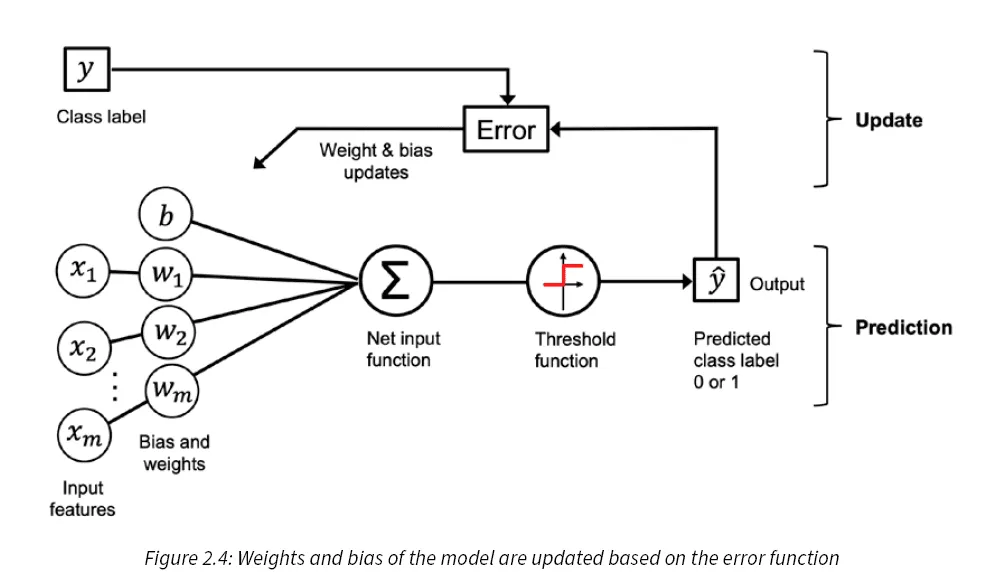
Ilustration of a Perceptron - early algorithm for supervised learning of various binary classification tasks

(source: Machine Learning with PyTorch and Scikit-Learn)

I remember feeling a sense of accomplishment when I first understood how the perceptron worked. But this was just the beginning.

Quickly after that, I learned about the Adaline model (Adaptive Linear Neuron) and this was where things started to get a bit more complicated.

Adaline vs. Perceptron: The key difference between Adaline (also known as the Widrow-Hoff rule or simply the Delta Learning Rule) and Rosenblatt’s perceptron is how the weights are updated. In Adaline, the weights are adjusted based on a linear activation function rather than a unit step function, which is used in the perceptron. Specifically, Adaline uses a linear activation function, 𝜎(𝑧) = 𝑧, which is simply the identity function of the net input.

This subtle change has a big implication: Adaline uses an algorithm called gradient descent for weight updates. I quickly realized that to fully grasp what was happening, I needed to understand gradient descent—a concept I never heard about before.

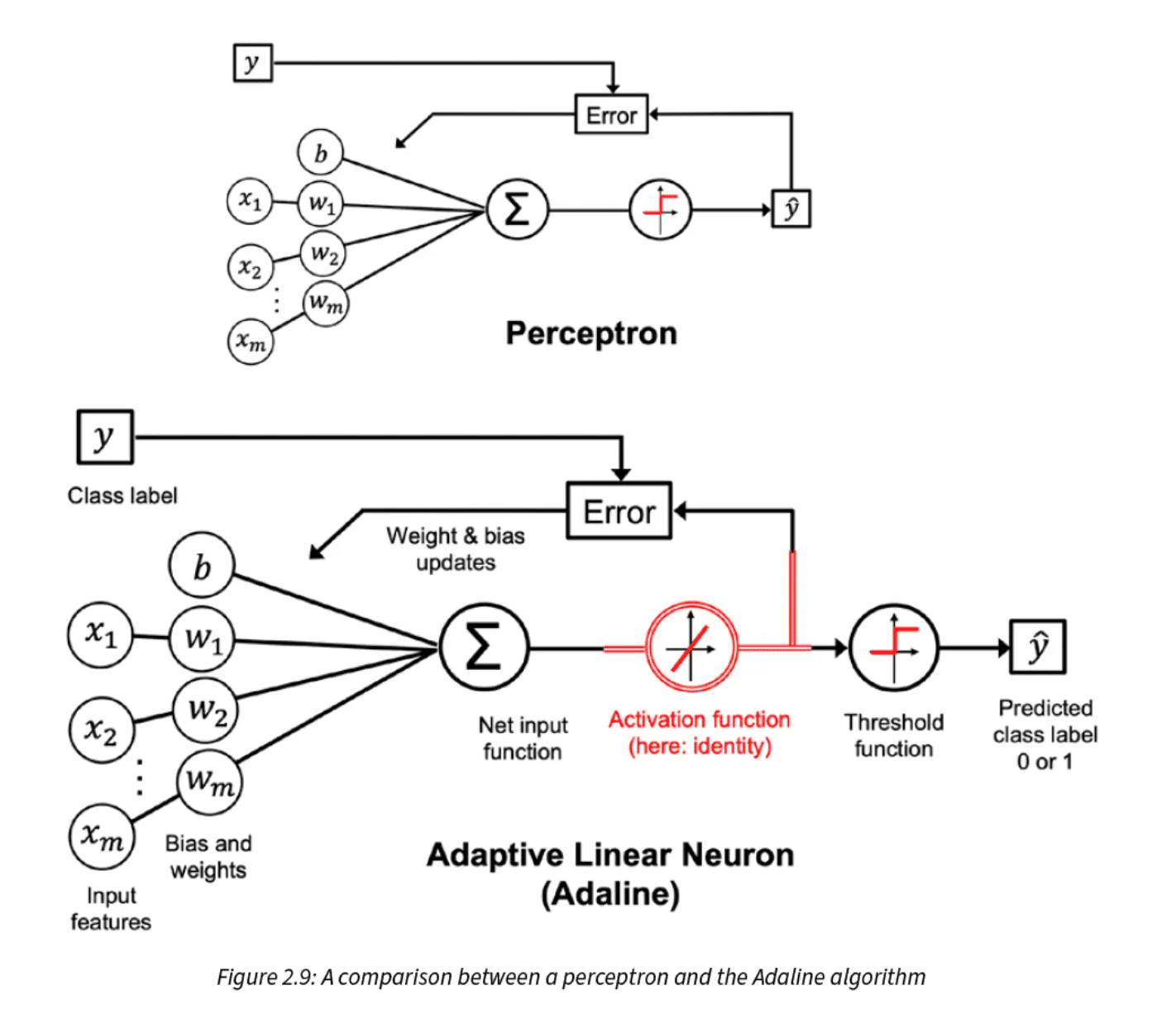
Graph of the Adaptive Linear Neuron - a single-layer artificial neural network

(source: Machine Learning with PyTorch and Scikit-Learn)

The Importance of Vector Calculus

No problem, I thought, let’s learn gradient descent. However, I soon found out that to truly understand gradient descent (and not just memorize the steps), I needed to dive into Vector Calculus.

  • Vector Calculus: Gradient descent involves calculating the gradient of a function, which is a vector that points in the direction of the steepest ascent. To minimize a function, you move in the opposite direction of the gradient. This concept is central to optimizing machine learning algorithms, but it’s rooted deeply in vector calculus.

This was a turning point for me. I started getting hints all over the place that math wasn’t just helpful—it was crucial for an in-depth understanding of machine learning.

But I faced a big question: How the hell do I learn math alone?!

Time For An Actual Learning Plan, I guess

The first thing I did was open Google and start searching for a math teacher. Since money wasn’t an issue, I thought hiring a tutor would be the fastest way to upskill. But things didn’t go as smoothly as I had hoped.

A few lessons in, I realized two major problems:

  1. Lack of Preparation: The tutor would start each lesson with, “What do you want to learn today?”—despite me having sent them the areas I wanted to cover beforehand. This approach felt disorganized and left me feeling more lost than before.

  2. Misaligned Teaching Style: Their explanations and analogies didn’t resonate with me. I quickly found that I was learning WAY faster by prompting ChatGPT than through the tutoring sessions.

Transitioning to Self-Learning

After firing the tutor and continuing to use ChatGPT, I soon realized that while LLMs are great at explaining concepts on the spot, they are TERRIBLE at ensuring I covered every essential topic in a particular math area.

This became painfully clear when I advanced to new lessons and found that areas I should have already mastered were completely foreign to me.

I knew I needed a more structured approach—something that would ensure I wasn’t skipping critical concepts.

Khan Academy Arc: I quickly stumbled upon Khan Academy. It seemed like the perfect solution at the time: it’s free, well-structured, and covers a wide range of topics. However, I soon encountered some limitations.

While the material is well-organized and easy to follow, I found that it lacked the depth and rigor needed to truly master the concepts.

The exercises were limited and not particularly challenging, which gave me a false sense of proficiency. I realized that I needed something more comprehensive to really test my understanding and push me further.

That’s when I decided to pick up a course or textbook to use as a guide.

Prof. Leonard’s Lectures: A Game-Changer

My search led me to Prof. Leonard’s lectures, which turned out to be a game-changer. I particularly liked Prof. Leonard’s teaching style and, of course, his buff physique!

His explanations were clear, and I felt like I was learning quickly and efficiently. It was smooth sailing for a while, and I was making good progress. But then, I realized another grave mistake I was making: I wasn’t practicing enough exercises at all.

The Importance of Practice

It’s easy to fall into the trap of thinking you understand material just because you can follow along with a lecture or video. But true mastery of mathematics comes from practice.

Without working through problems on your own, it’s impossible to solidify the concepts in your mind or to apply them effectively.

Watching videos or attending lectures gives you a false sense of confidence—it’s the practice that builds real skill.

Finding the Right Textbook

Realizing the need for more practice, I asked around and tested a few textbooks. Eventually, I landed on Ron Larson’s Calculus textbook, which I really liked.

The explanations were clear and well-structured, and they synced perfectly with Prof. Leonard’s lessons. This combination became my new roadmap for learning.

Conclusion

I continued with Prof. Leonard’s lectures and Ron Larson’s textbook until I eventually switched to Math Academy.

At the time of writing this, Math Academy is my go-to resource for learning math.

The journey hasn’t been a straight line, but by combining structured resources with plenty of practice, I’m slowly starting to feel confident in my math skills.

Appreciate you reading to the end! :)